Skip to contents

EM MAP for mixture of sNiW

Source: R/MAP_sNiW_mmEM.R
MAP_sNiW_mmEM.Rd

Maximum A Posteriori (MAP) estimation of mixture of Normal inverse Wishart distributed observations with an EM algorithm

Usage

MAP_sNiW_mmEM(
  xi_list,
  psi_list,
  S_list,
  hyperG0,
  init = NULL,
  K,
  maxit = 100,
  tol = 0.1,
  doPlot = TRUE,
  verbose = TRUE
)

MAP_sNiW_mmEM_weighted(
  xi_list,
  psi_list,
  S_list,
  obsweight_list,
  hyperG0,
  K,
  maxit = 100,
  tol = 0.1,
  doPlot = TRUE,
  verbose = TRUE
)

MAP_sNiW_mmEM_vague(
  xi_list,
  psi_list,
  S_list,
  hyperG0,
  K = 10,
  maxit = 100,
  tol = 0.1,
  doPlot = TRUE,
  verbose = TRUE
)

Arguments

xi_list

a list of length n, each element is a vector of size d containing the argument xi of the corresponding allocated cluster.

psi_list

a list of length n, each element is a vector of size d containing the argument psi of the corresponding allocated cluster.

S_list

a list of length n, each element is a matrix of size d x d containing the argument S of the corresponding allocated cluster.

hyperG0

prior mixing distribution used if init is NULL.

init

a list for initializing the algorithm with the following elements: b_xi, b_psi, lambda, B, nu. Default is NULL in which case the initialization of the algorithm is random.

K

integer giving the number of mixture components.

maxit

integer giving the maximum number of iteration for the EM algorithm. Default is 100.

tol

real number giving the tolerance for the stopping of the EM algorithm. Default is 0.1.

doPlot

a logical flag indicating whether the algorithm progression should be plotted. Default is TRUE.

verbose

logical flag indicating whether plot should be drawn. Default is TRUE.

obsweight_list

a list of length n where each element is a vector of weights for each sampled cluster at each MCMC iterations.

Details

MAP_sNiW_mmEM provides an estimation for the MAP of mixtures of Normal inverse Wishart distributed observations. MAP_sNiW_mmEM_vague provides an estimates incorporating a vague component in the mixture. MAP_sNiW_mmEM_weighted provides a weighted version of the algorithm.

Author

Boris Hejblum, Chariff Alkhassim

Examples

set.seed(1234)
hyperG0 <- list()
hyperG0$b_xi <- c(0.3, -1.5)
hyperG0$b_psi <- c(0, 0)
hyperG0$kappa <- 0.001
hyperG0$D_xi <- 100
hyperG0$D_psi <- 100
hyperG0$nu <- 20
hyperG0$lambda <- diag(c(0.25,0.35))

hyperG0 <- list()
hyperG0$b_xi <- c(1, -1.5)
hyperG0$b_psi <- c(0, 0)
hyperG0$kappa <- 0.1
hyperG0$D_xi <- 1
hyperG0$D_psi <- 1
hyperG0$nu <- 2
hyperG0$lambda <- diag(c(0.25,0.35))

xi_list <- list()
psi_list <- list()
S_list <- list()
w_list <- list()

for(k in 1:200){
 NNiW <- rNNiW(hyperG0, diagVar=FALSE)
 xi_list[[k]] <- NNiW[["xi"]]
 psi_list[[k]] <- NNiW[["psi"]]
 S_list[[k]] <- NNiW[["S"]]
 w_list [[k]] <- 0.75
}


hyperG02 <- list()
hyperG02$b_xi <- c(-1, 2)
hyperG02$b_psi <- c(-0.1, 0.5)
hyperG02$kappa <- 0.1
hyperG02$D_xi <- 1
hyperG02$D_psi <- 1
hyperG02$nu <- 4
hyperG02$lambda <- 0.5*diag(2)

for(k in 201:400){
 NNiW <- rNNiW(hyperG02, diagVar=FALSE)
 xi_list[[k]] <- NNiW[["xi"]]
 psi_list[[k]] <- NNiW[["psi"]]
 S_list[[k]] <- NNiW[["S"]]
 w_list [[k]] <- 0.25

}

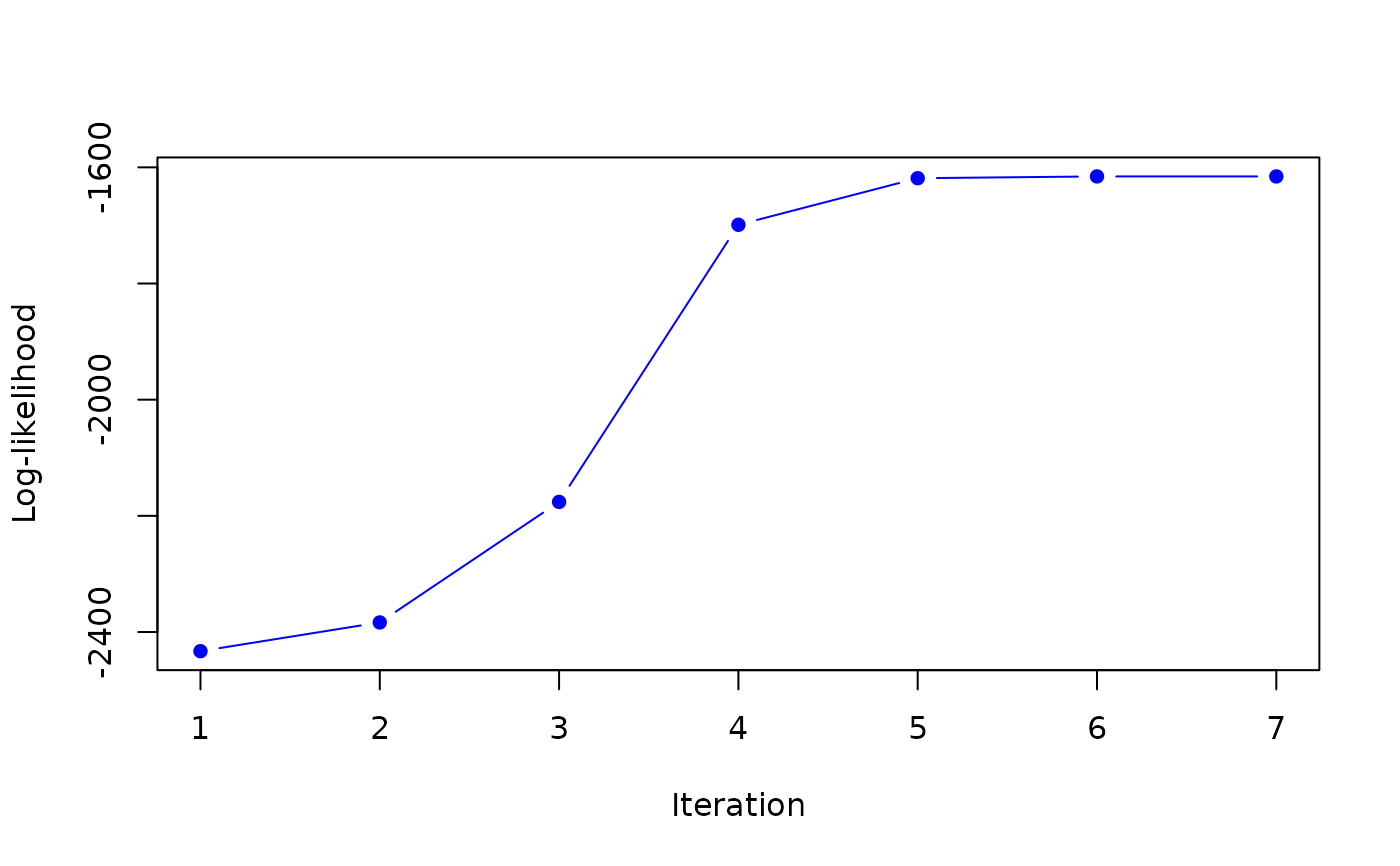
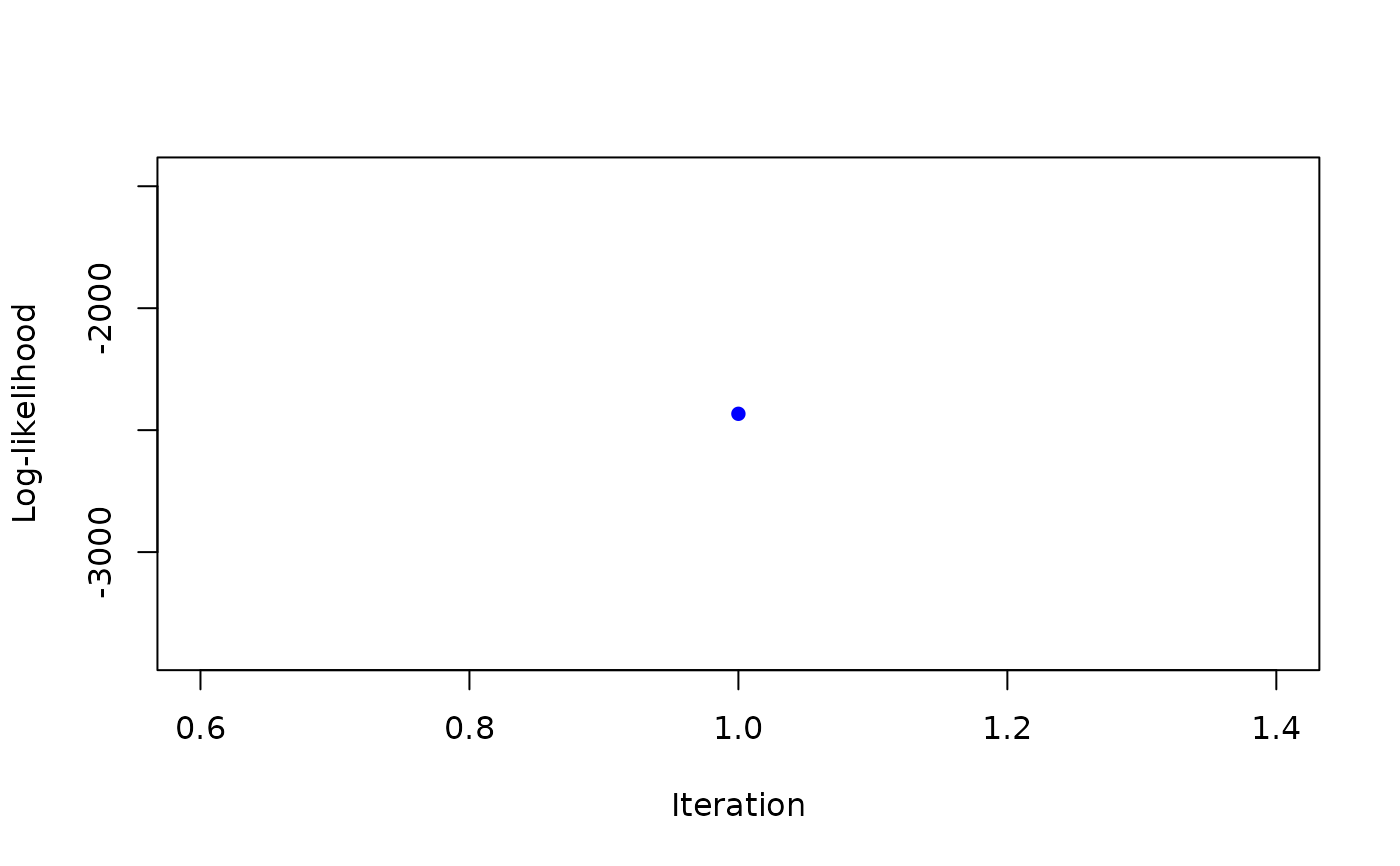
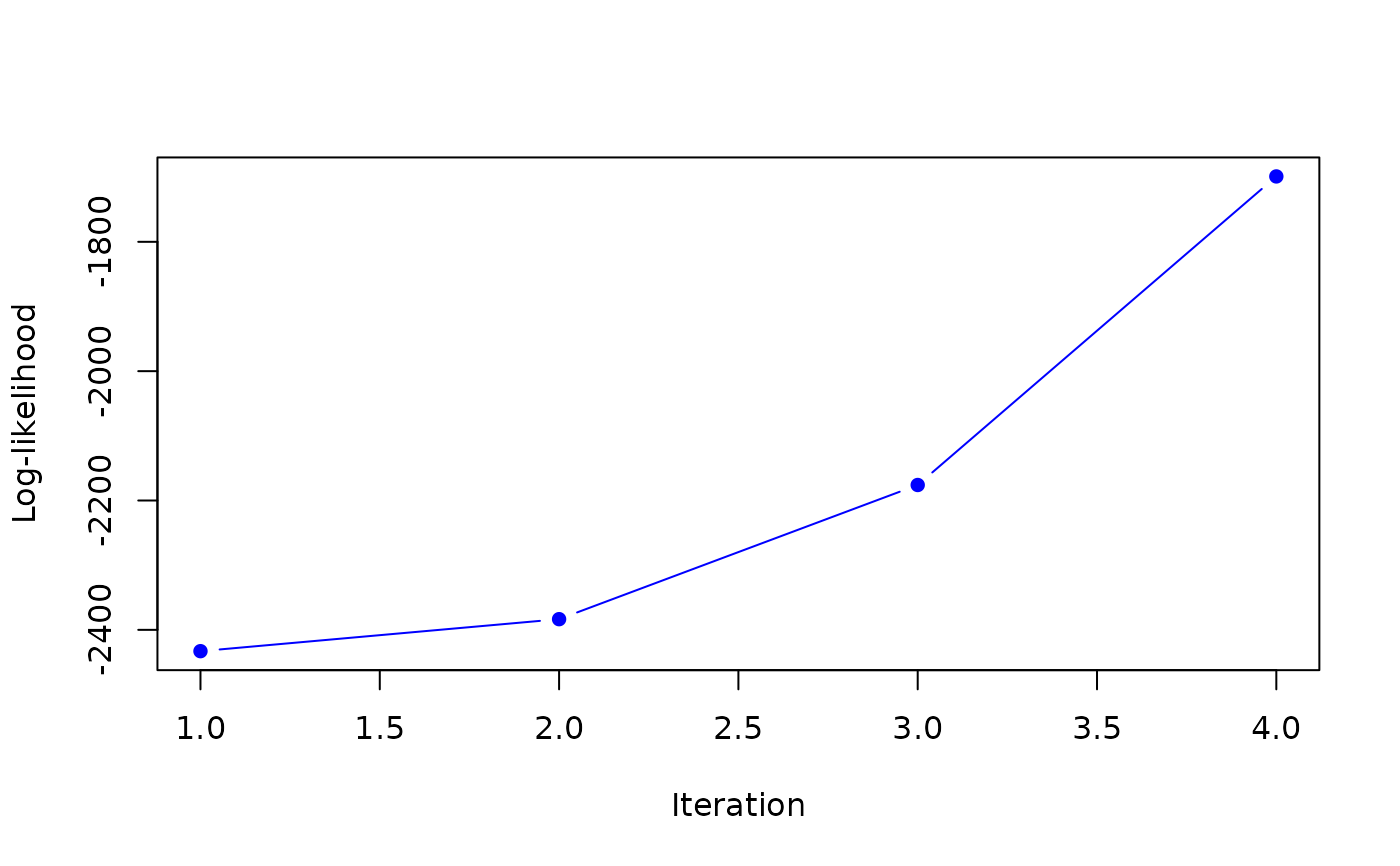
map <- MAP_sNiW_mmEM(xi_list, psi_list, S_list, hyperG0, K=2, tol=0.1)
#> it 1: loglik = -2432.972
#> weights: 0.2966973 0.7033027 
#> 

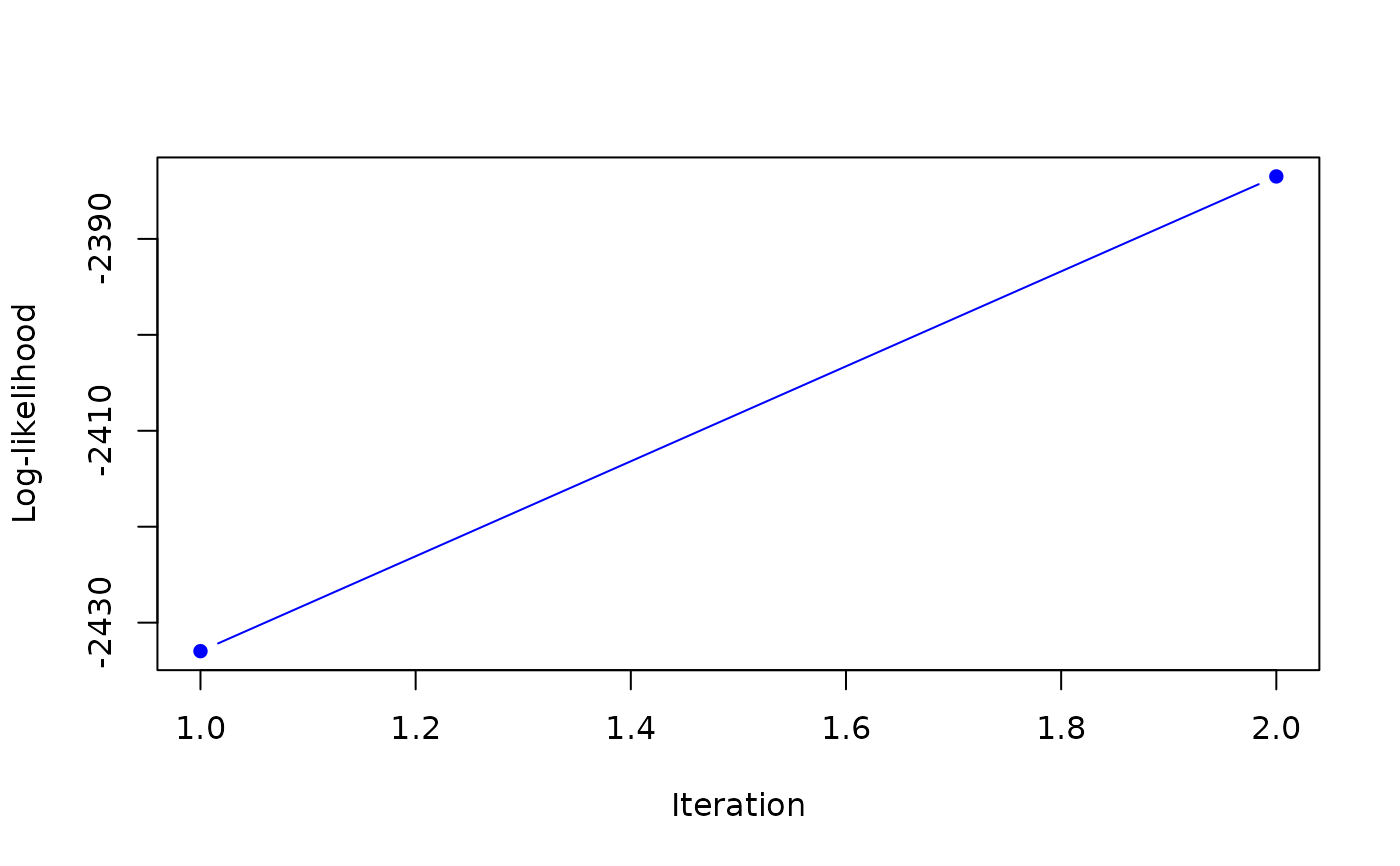
#> it 2: loglik = -2383.489
#> weights: 0.3230128 0.6769872 
#> 

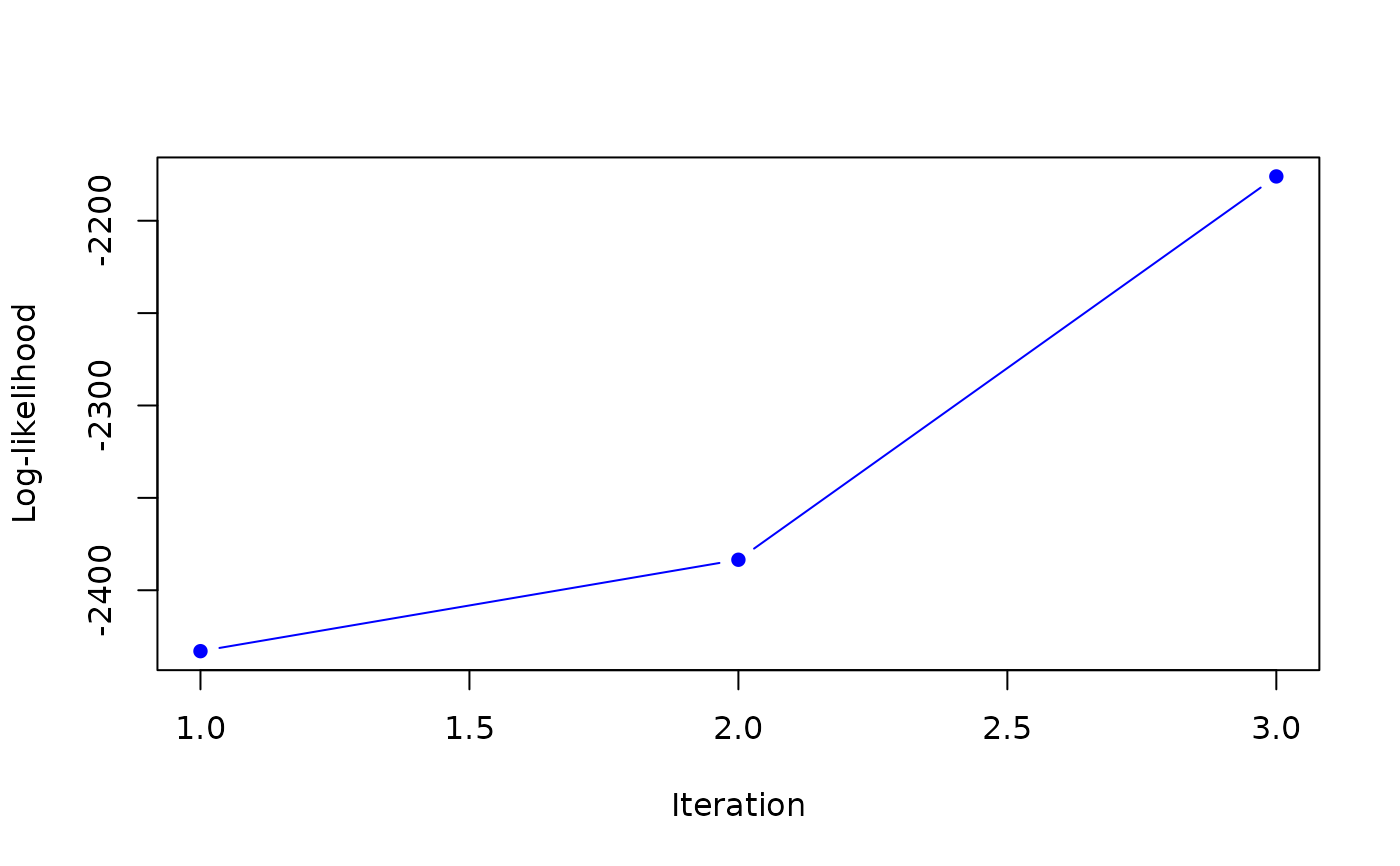
#> it 3: loglik = -2176.02
#> weights: 0.3674474 0.6325526 
#> 

#> it 4: loglik = -1698.888
#> weights: 0.4293908 0.5706092 
#> 

#> it 5: loglik = -1618.705
#> weights: 0.4831102 0.5168898 
#> 

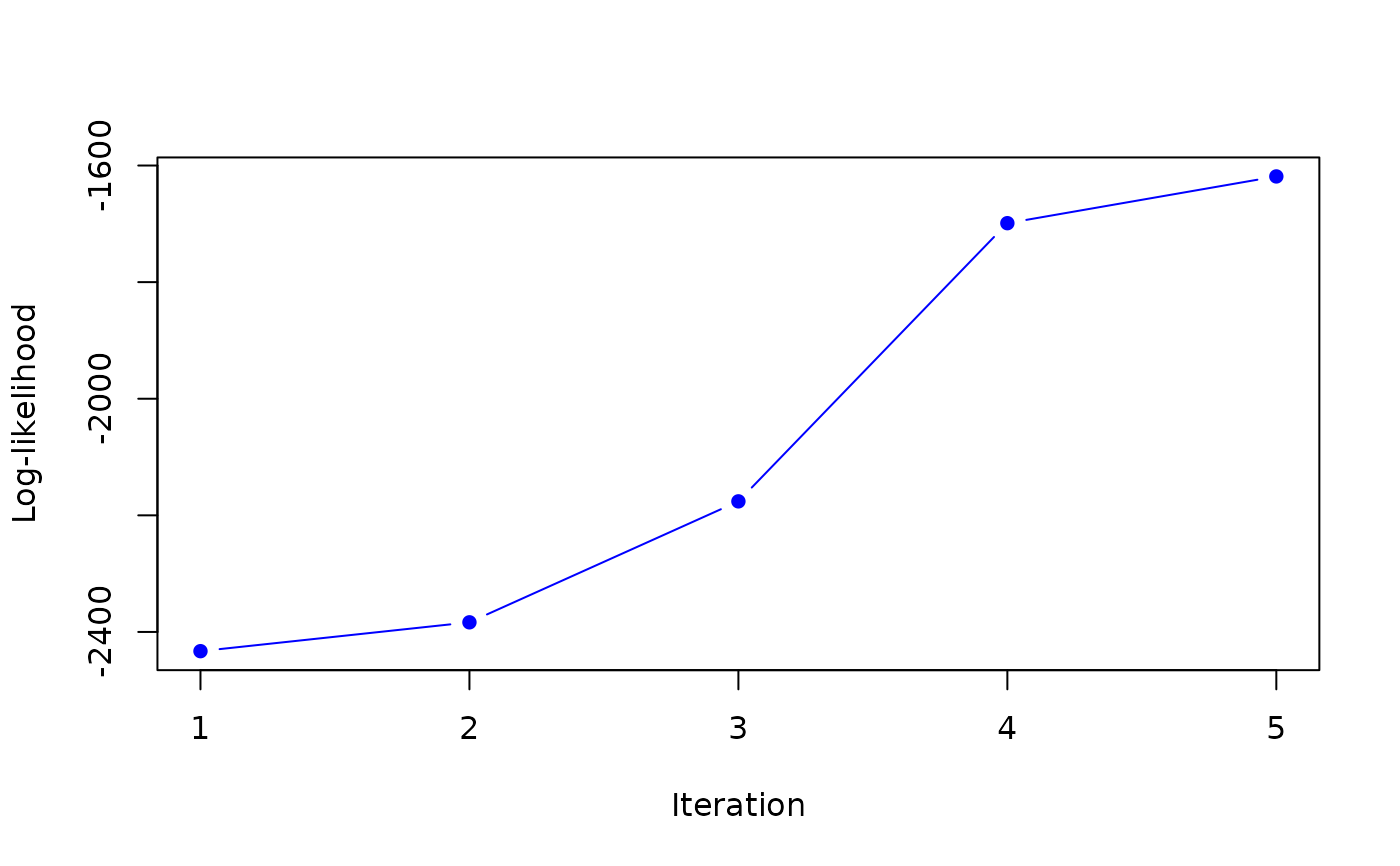#> it 6: loglik = -1615.645
#> weights: 0.4954632 0.5045368 
#> 

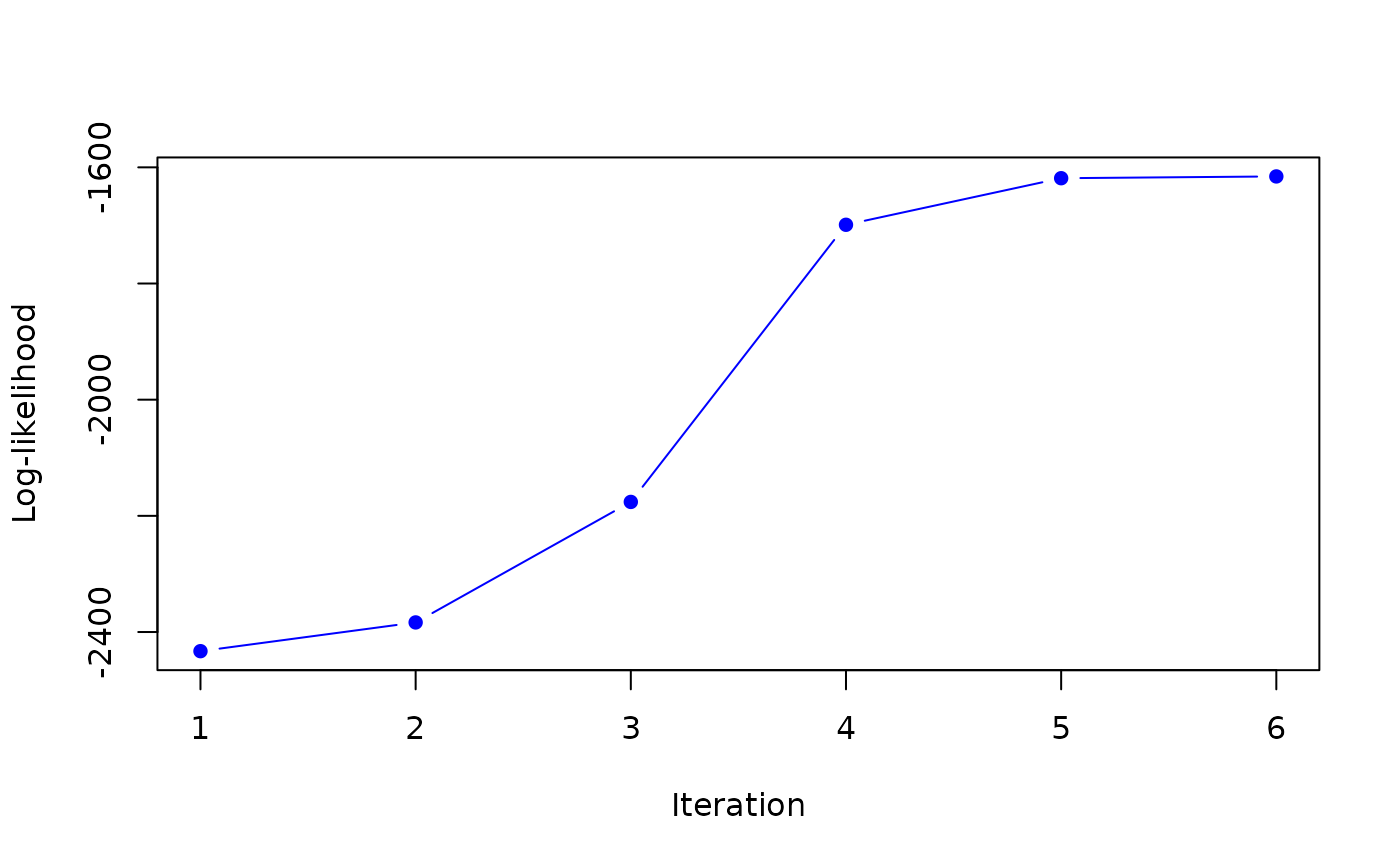#> it 7: loglik = -1615.66
#> weights: 0.497025 0.502975 
#>