Skip to contents

EM MLE for mixture of NiW

Source: R/MLE_sNiW_mmEM.R
MLE_NiW_mmEM.Rd

Maximum likelihood estimation of mixture of Normal inverse Wishart distributed observations with an EM algorithm

Usage

MLE_NiW_mmEM(
  mu_list,
  S_list,
  hyperG0,
  K,
  maxit = 100,
  tol = 0.1,
  doPlot = TRUE
)

Arguments

mu_list

a list of length N whose elements are observed vectors of length d of the mean parameters.

S_list

a list of length N whose elements are observed variance-covariance matrices of dimension d x d.

hyperG0

prior mixing distribution used for randomly initializing the algorithm.

K

integer giving the number of mixture components.

maxit

integer giving the maximum number of iteration for the EM algorithm. Default is 100.

tol

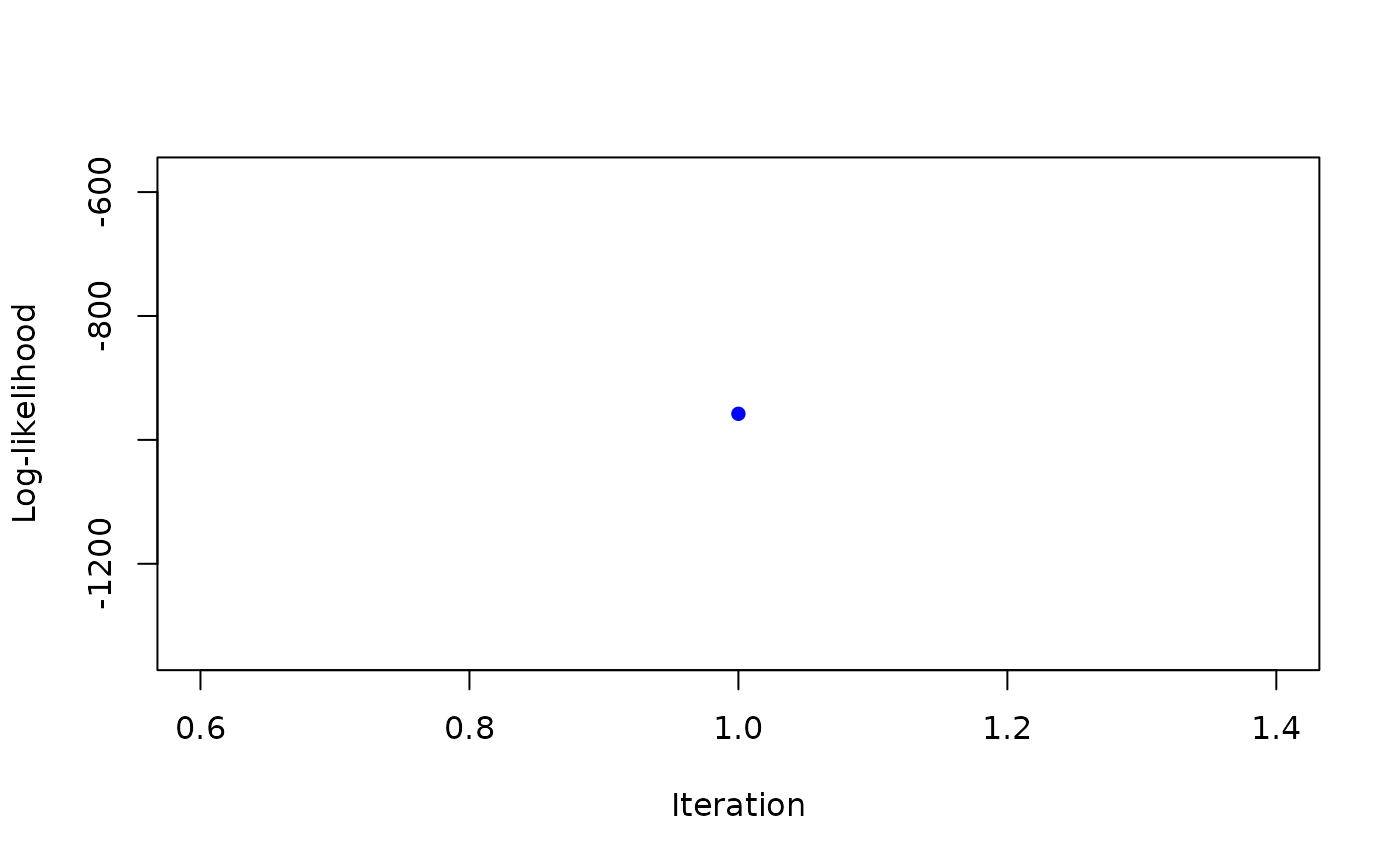
real number giving the tolerance for the stopping of the EM algorithm. Default is 0.1.

doPlot

a logical flag indicating whether the algorithm progression should be plotted. Default is TRUE.

Examples

set.seed(123)
U_mu <- list()
U_Sigma <- list()
U_nu<-list()
U_kappa<-list()

d <- 2
hyperG0 <- list()
hyperG0[["mu"]] <- rep(1,d)
hyperG0[["kappa"]] <- 0.01
hyperG0[["nu"]] <- d+1
hyperG0[["lambda"]] <- diag(d)

for(k in 1:200){

  NiW <- rNiW(hyperG0, diagVar=FALSE)
  U_mu[[k]] <-NiW[["mu"]]
  U_Sigma[[k]] <-NiW[["S"]]
}


hyperG02 <- list()
hyperG02[["mu"]] <- rep(2,d)
hyperG02[["kappa"]] <- 1
hyperG02[["nu"]] <- d+10
hyperG02[["lambda"]] <- diag(d)/10

for(k in 201:400){

  NiW <- rNiW(hyperG02, diagVar=FALSE)
  U_mu[[k]] <-NiW[["mu"]]
  U_Sigma[[k]] <-NiW[["S"]]
}


mle <- MLE_NiW_mmEM( U_mu, U_Sigma, hyperG0, K=2)






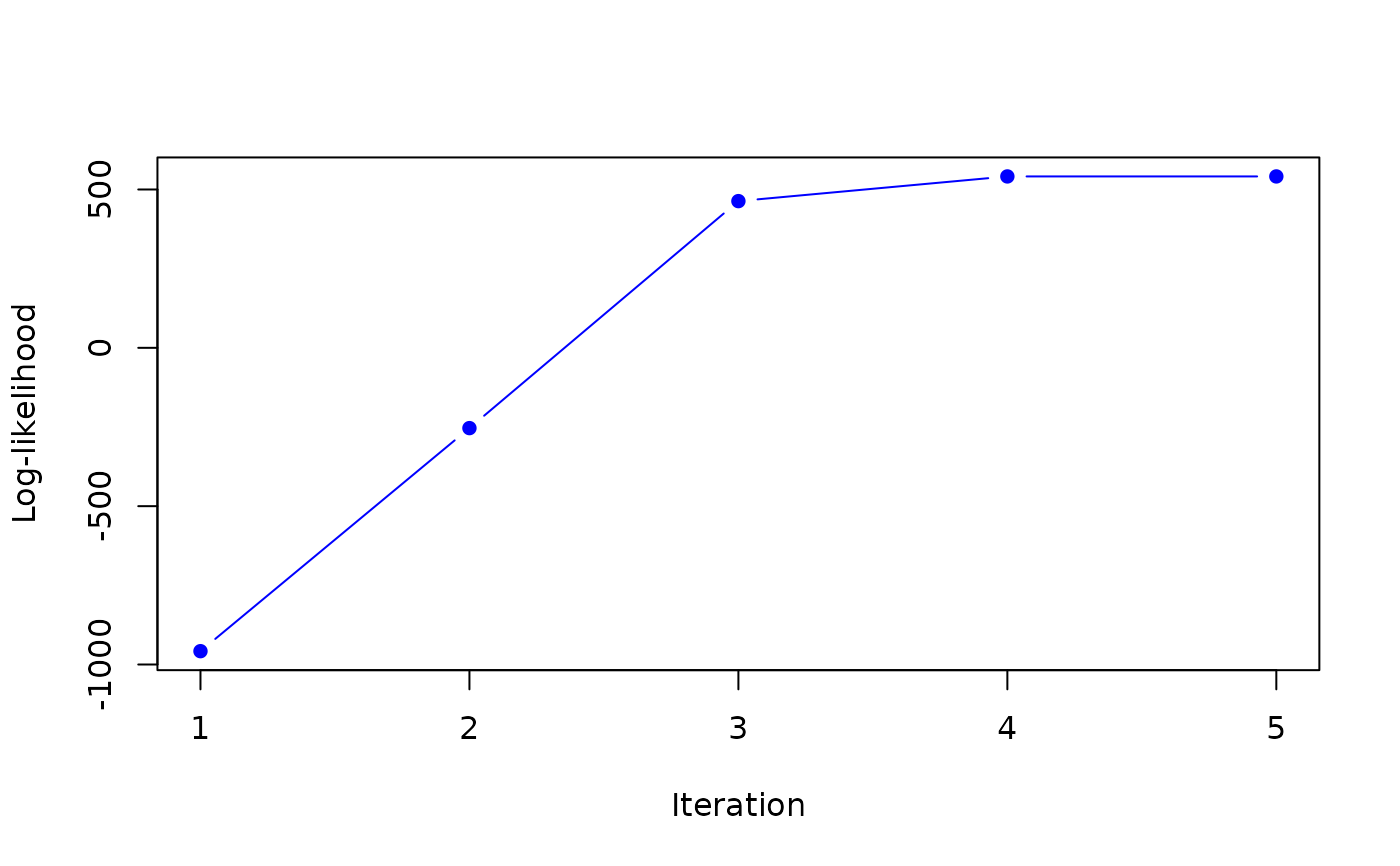hyperG0[["mu"]]
#> [1] 1 1
hyperG02[["mu"]]
#> [1] 2 2
mle$U_mu
#> [[1]]
#>          [,1]    [,2]
#> [1,] 1.999416 1.99535
#> 
#> [[2]]
#>           [,1]      [,2]
#> [1,] 0.6043477 0.7329735
#> 

hyperG0[["lambda"]]
#>      [,1] [,2]
#> [1,]    1    0
#> [2,]    0    1
hyperG02[["lambda"]]
#>      [,1] [,2]
#> [1,]  0.1  0.0
#> [2,]  0.0  0.1
mle$U_lambda
#> [[1]]
#>               [,1]          [,2]
#> [1,]  0.0979444365 -0.0007475601
#> [2,] -0.0007475601  0.1023912997
#> 
#> [[2]]
#>             [,1]        [,2]
#> [1,]  1.09929757 -0.01653896
#> [2,] -0.01653896  1.01996818
#> 

hyperG0[["nu"]]
#> [1] 3
hyperG02[["nu"]]
#> [1] 12
mle$U_nu
#> [[1]]
#> [1] 12
#> 
#> [[2]]
#> [1] 3
#> 

hyperG0[["kappa"]]
#> [1] 0.01
hyperG02[["kappa"]]
#> [1] 1
mle$U_kappa
#> [[1]]
#> [1] 1.039521
#> 
#> [[2]]
#> [1] 0.009574888
#>