Skip to contents

EM MLE for mixture of sNiW

Source: R/MLE_sNiW_mmEM.R
MLE_sNiW_mmEM.Rd

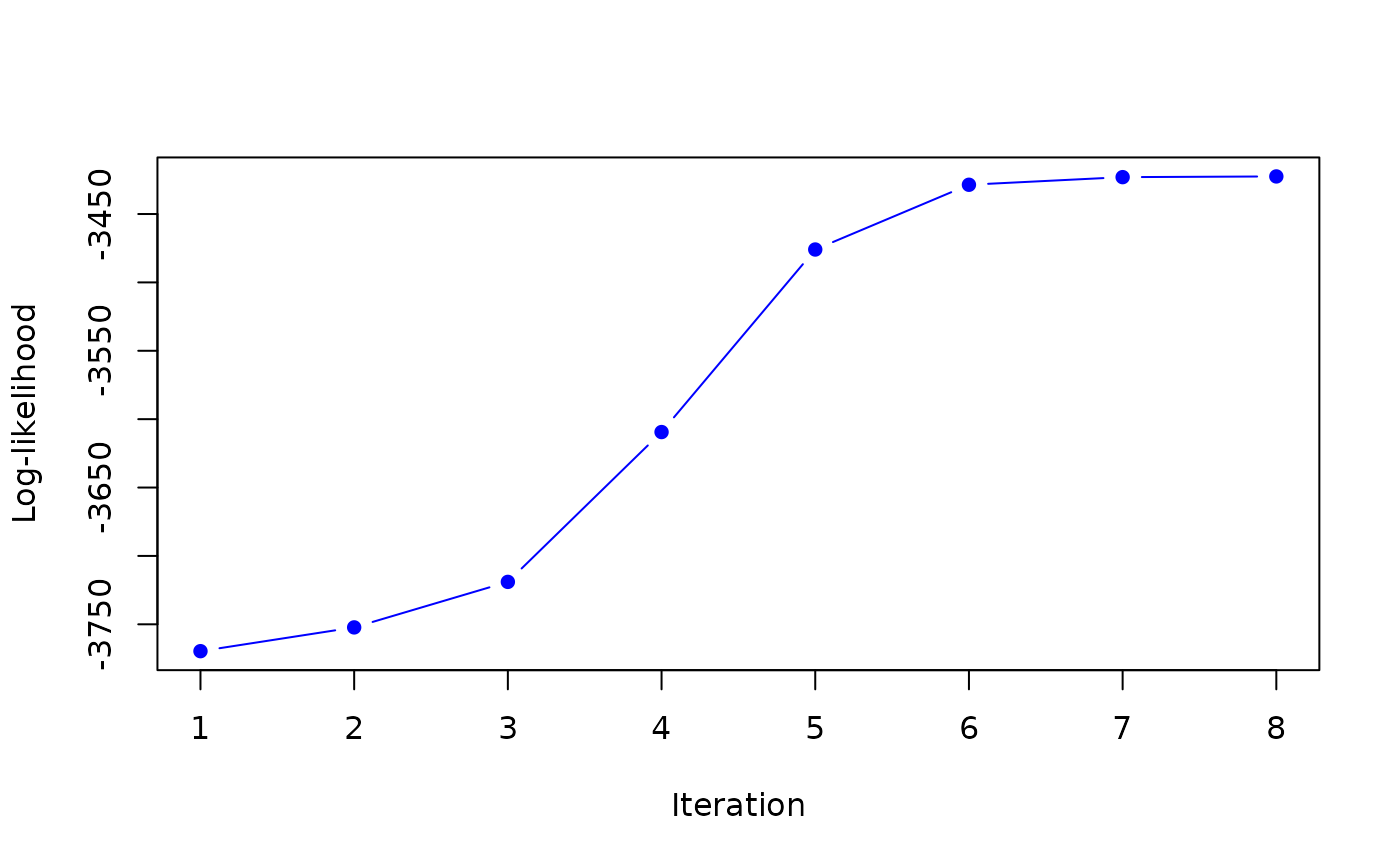
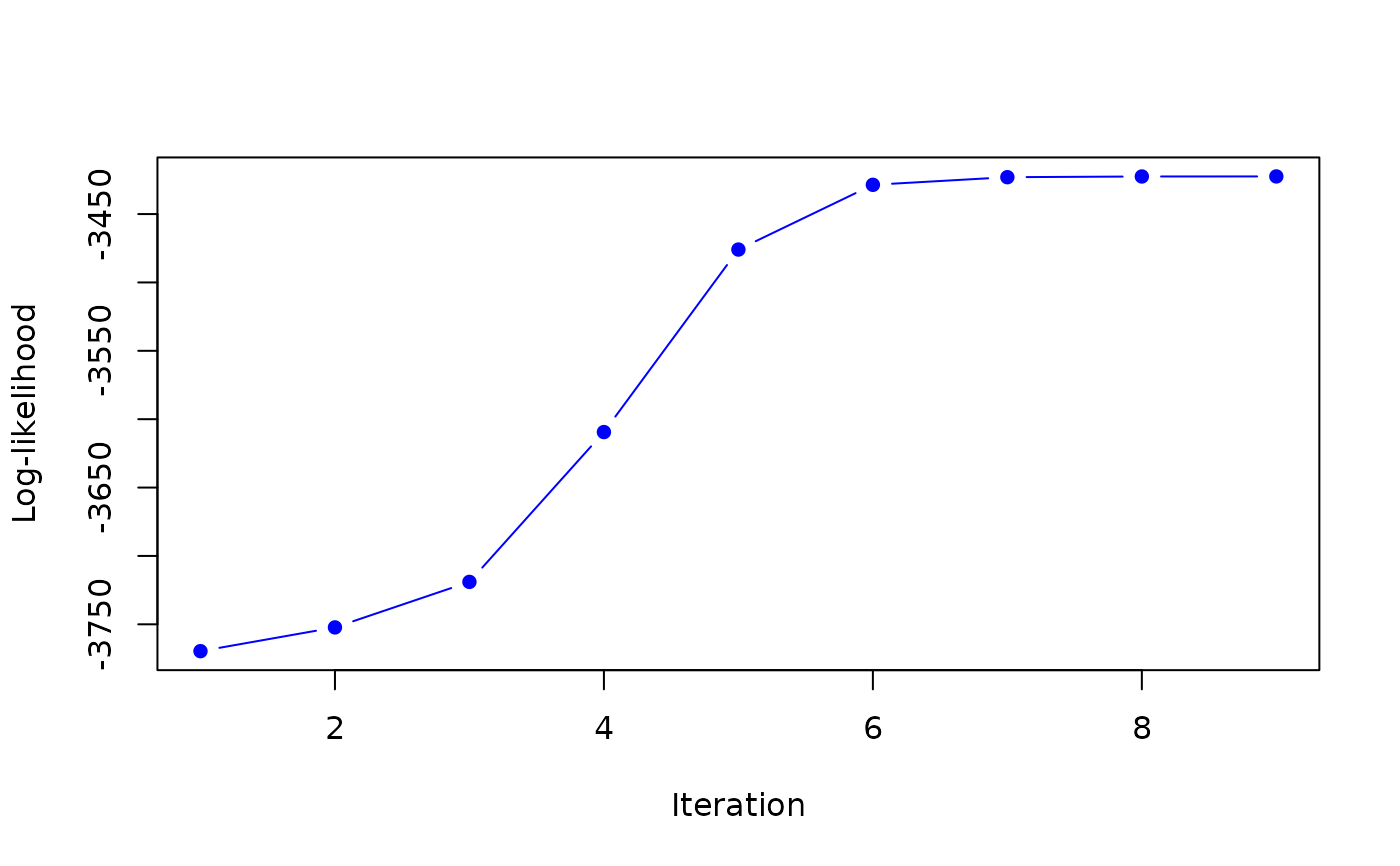
Maximum likelihood estimation of mixture of Normal inverse Wishart distributed observations with an EM algorithm

Usage

MLE_sNiW_mmEM(
  xi_list,
  psi_list,
  S_list,
  hyperG0,
  K,
  init = NULL,
  maxit = 100,
  tol = 0.1,
  doPlot = TRUE,
  verbose = TRUE
)

Arguments

xi_list

a list of length N whose elements are observed vectors of length d of the mean parameters xi.

psi_list

a list of length N whose elements are observed vectors of length d of the skew parameters psi.

S_list

a list of length N whose elements are observed variance-covariance matrices of dimension d x d.

hyperG0

prior mixing distribution used if init is NULL.

K

integer giving the number of mixture components.

init

a list for initializing the algorithm with the following elements: b_xi, b_psi, lambda, B, nu. Default is NULL in which case the initialization of the algorithm is random.

maxit

integer giving the maximum number of iteration for the EM algorithm. Default is 100.

tol

real number giving the tolerance for the stopping of the EM algorithm. Default is 0.1.

doPlot

a logical flag indicating whether the algorithm progression should be plotted. Default is TRUE.

verbose

logical flag indicating whether plot should be drawn. Default is TRUE.

Author

Boris Hejblum, Chariff Alkhassim

Examples

set.seed(1234)
hyperG0 <- list()
hyperG0$b_xi <- c(0.3, -1.5)
hyperG0$b_psi <- c(0, 0)
hyperG0$kappa <- 0.001
hyperG0$D_xi <- 100
hyperG0$D_psi <- 100
hyperG0$nu <- 3
hyperG0$lambda <- diag(c(0.25,0.35))

xi_list <- list()
psi_list <- list()
S_list <- list()
for(k in 1:200){
 NNiW <- rNNiW(hyperG0, diagVar=FALSE)
 xi_list[[k]] <- NNiW[["xi"]]
 psi_list[[k]] <- NNiW[["psi"]]
 S_list[[k]] <- NNiW[["S"]]
}

hyperG02 <- list()
hyperG02$b_xi <- c(-1, 2)
hyperG02$b_psi <- c(-0.1, 0.5)
hyperG02$kappa <- 0.001
hyperG02$D_xi <- 10
hyperG02$D_psi <- 10
hyperG02$nu <- 3
hyperG02$lambda <- 0.5*diag(2)

for(k in 201:400){
 NNiW <- rNNiW(hyperG02, diagVar=FALSE)
 xi_list[[k]] <- NNiW[["xi"]]
 psi_list[[k]] <- NNiW[["psi"]]
 S_list[[k]] <- NNiW[["S"]]
}

mle <- MLE_sNiW_mmEM(xi_list, psi_list, S_list, hyperG0, K=2)
#> it 1: loglik = -3769.643
#> weights: 0.4176288 0.5823712 
#> 

#> it 2: loglik = -3752.259
#> weights: 0.391004 0.608996 
#> 

#> it 3: loglik = -3718.983
#> weights: 0.3950537 0.6049463 
#> 

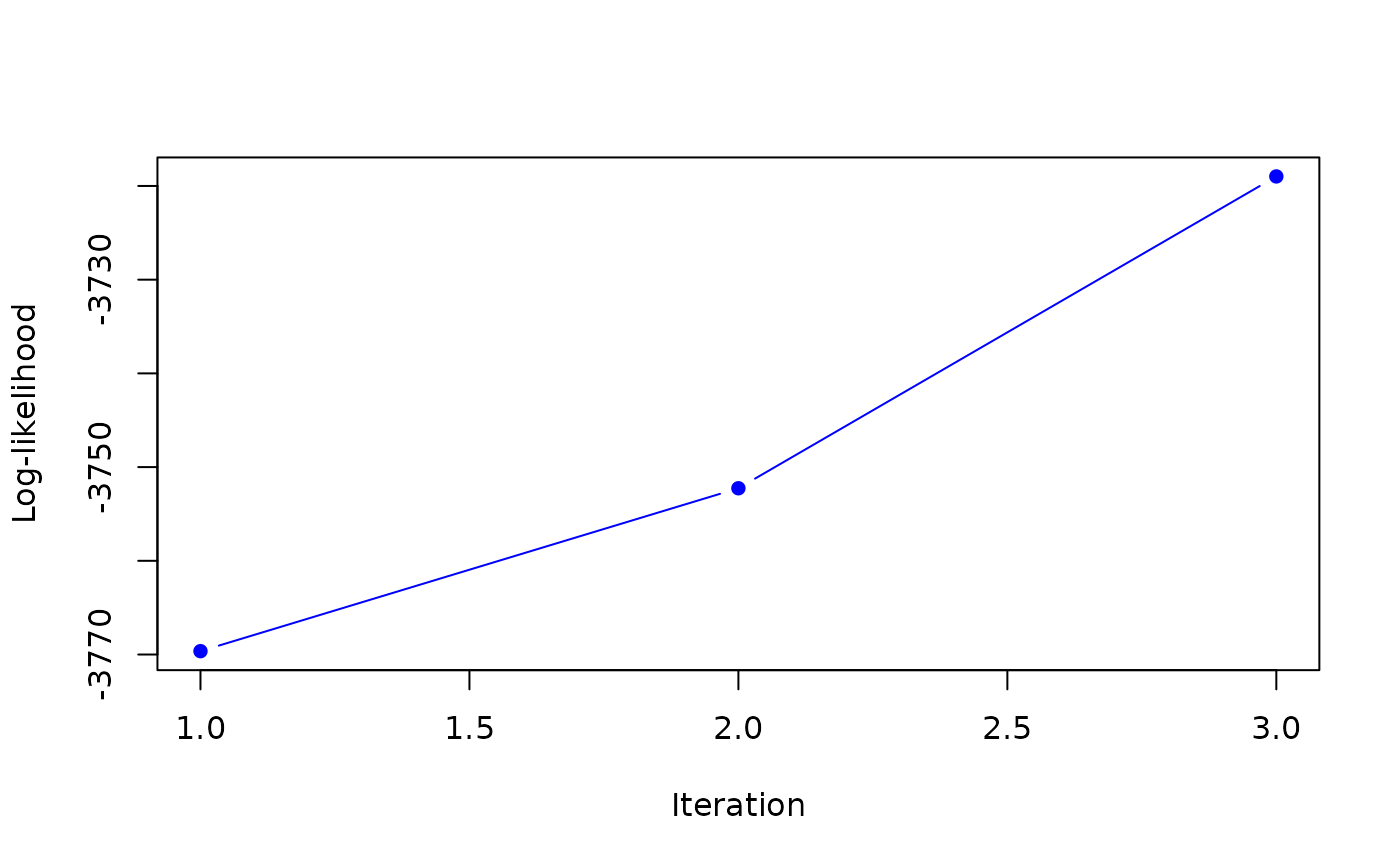#> it 4: loglik = -3609.423
#> weights: 0.4242218 0.5757782 
#> 

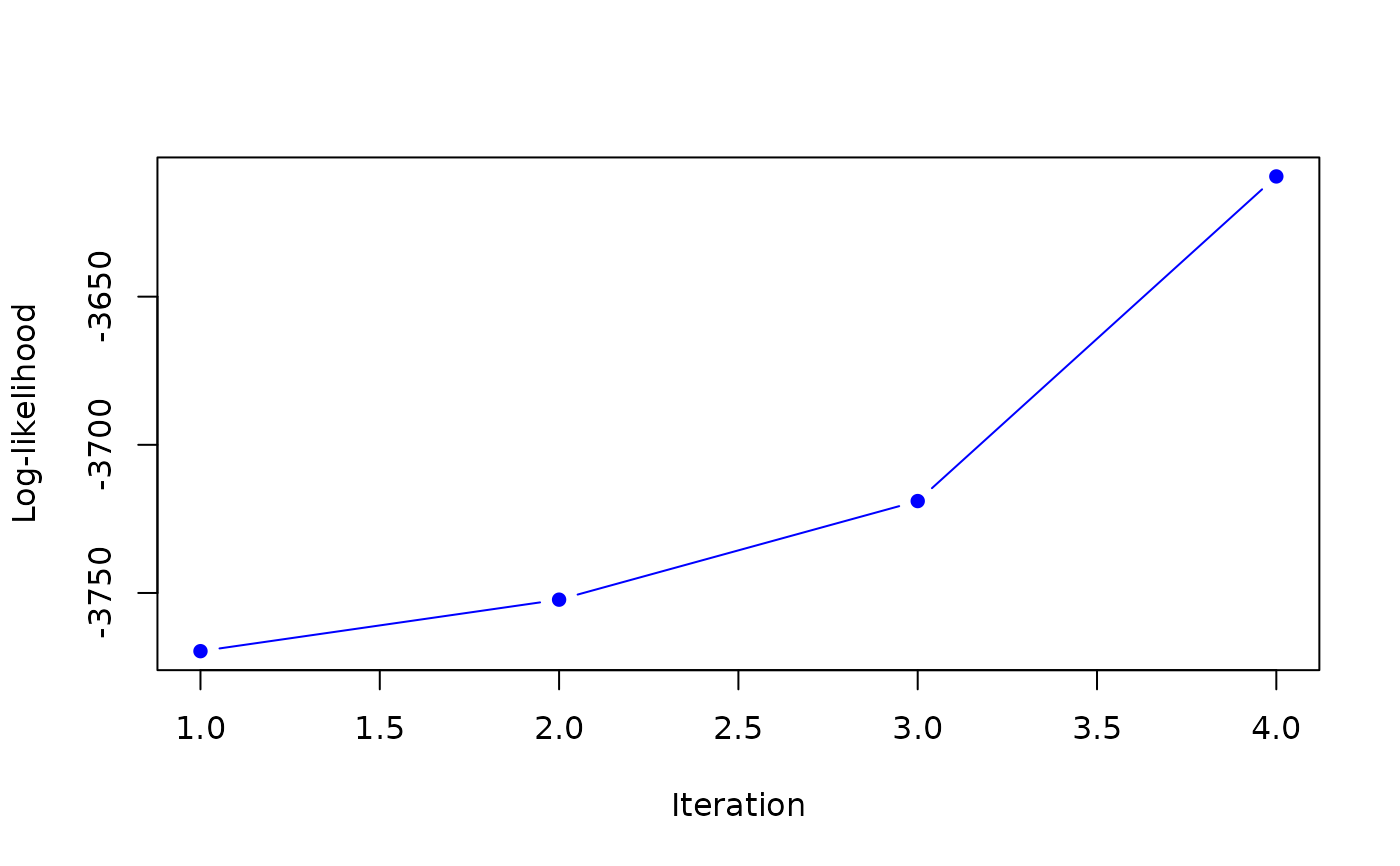#> it 5: loglik = -3475.95
#> weights: 0.4839074 0.5160926 
#> 

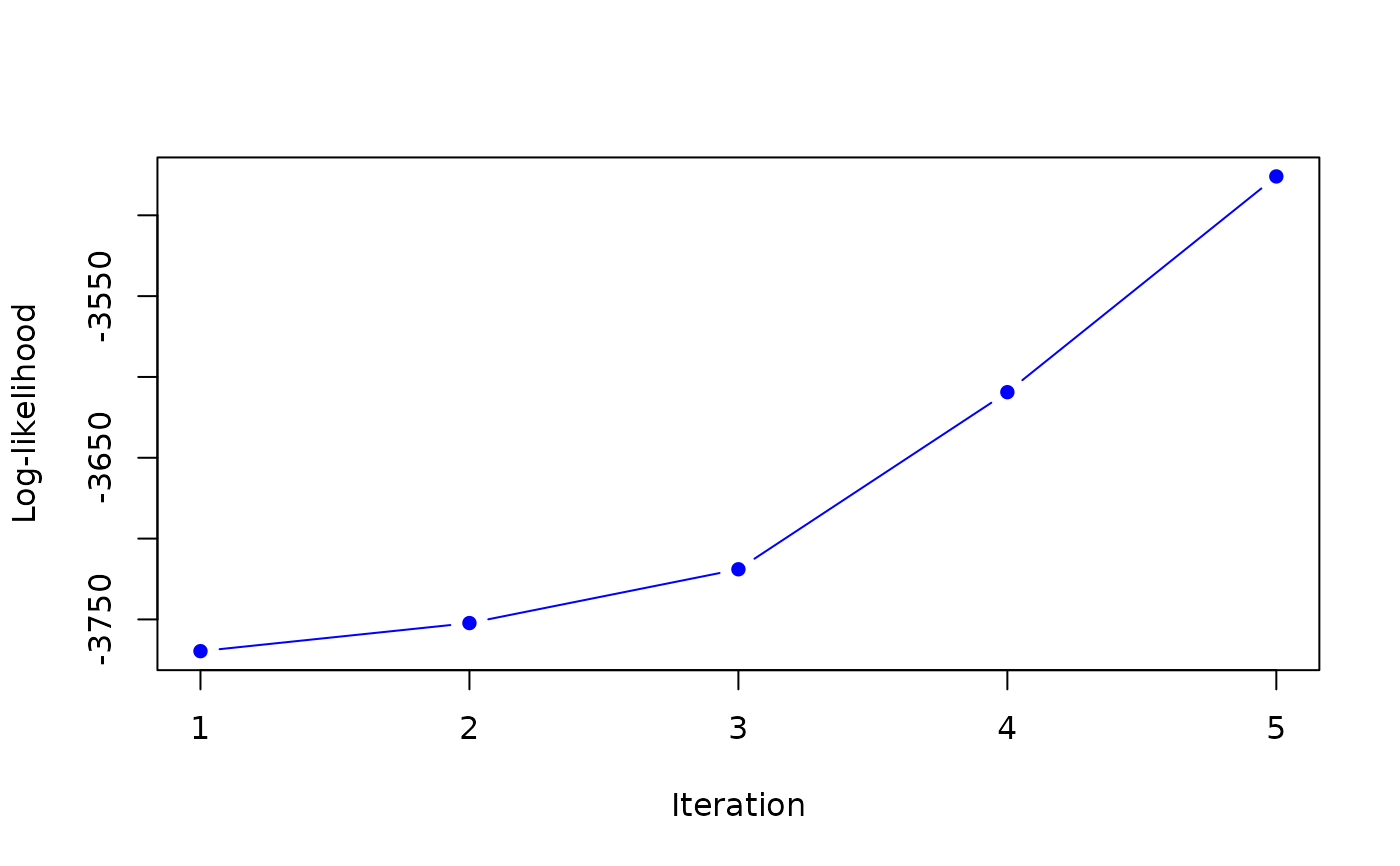#> it 6: loglik = -3428.609
#> weights: 0.50906 0.49094 
#> 

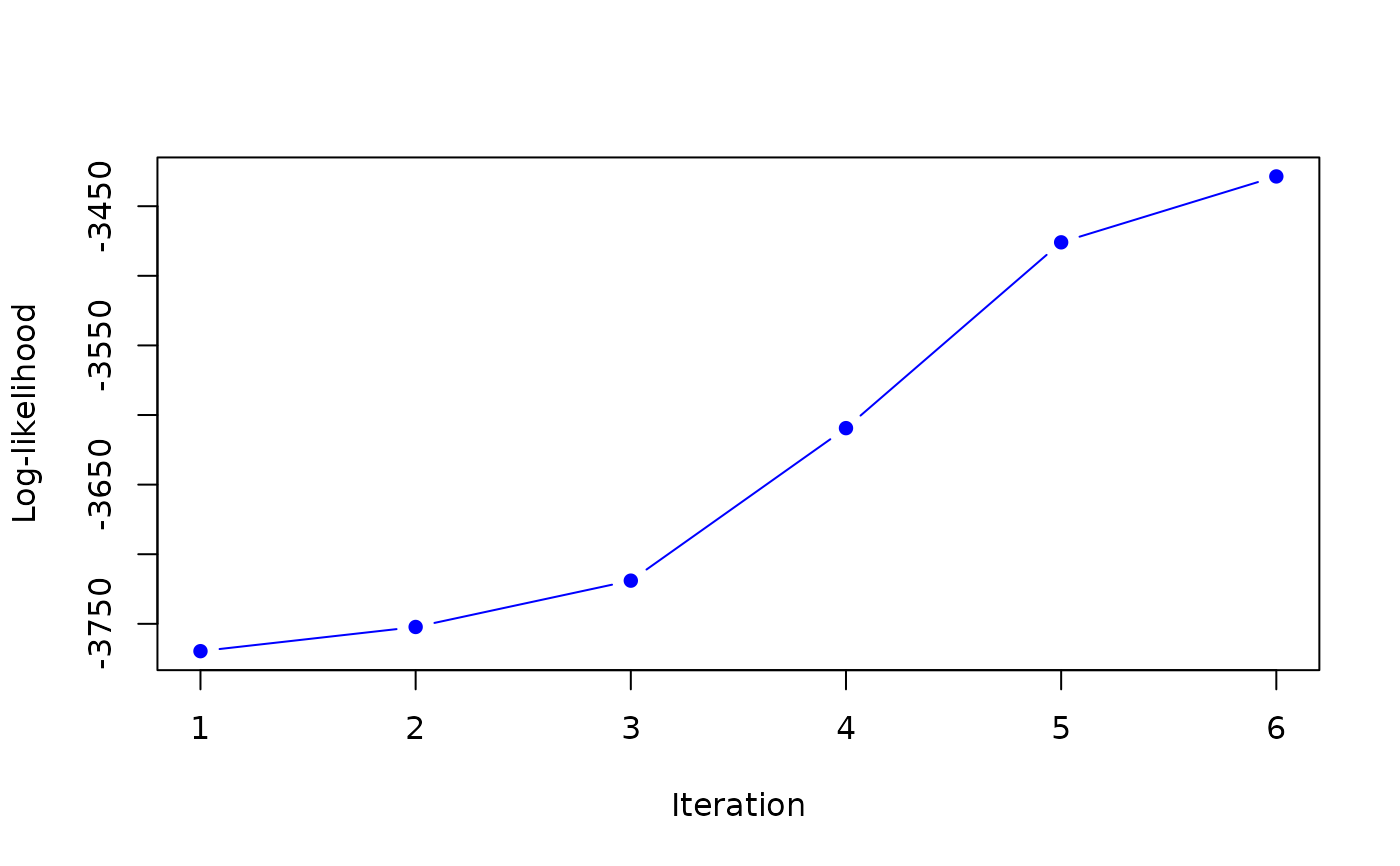#> it 7: loglik = -3423.035
#> weights: 0.5037029 0.4962971 
#> 

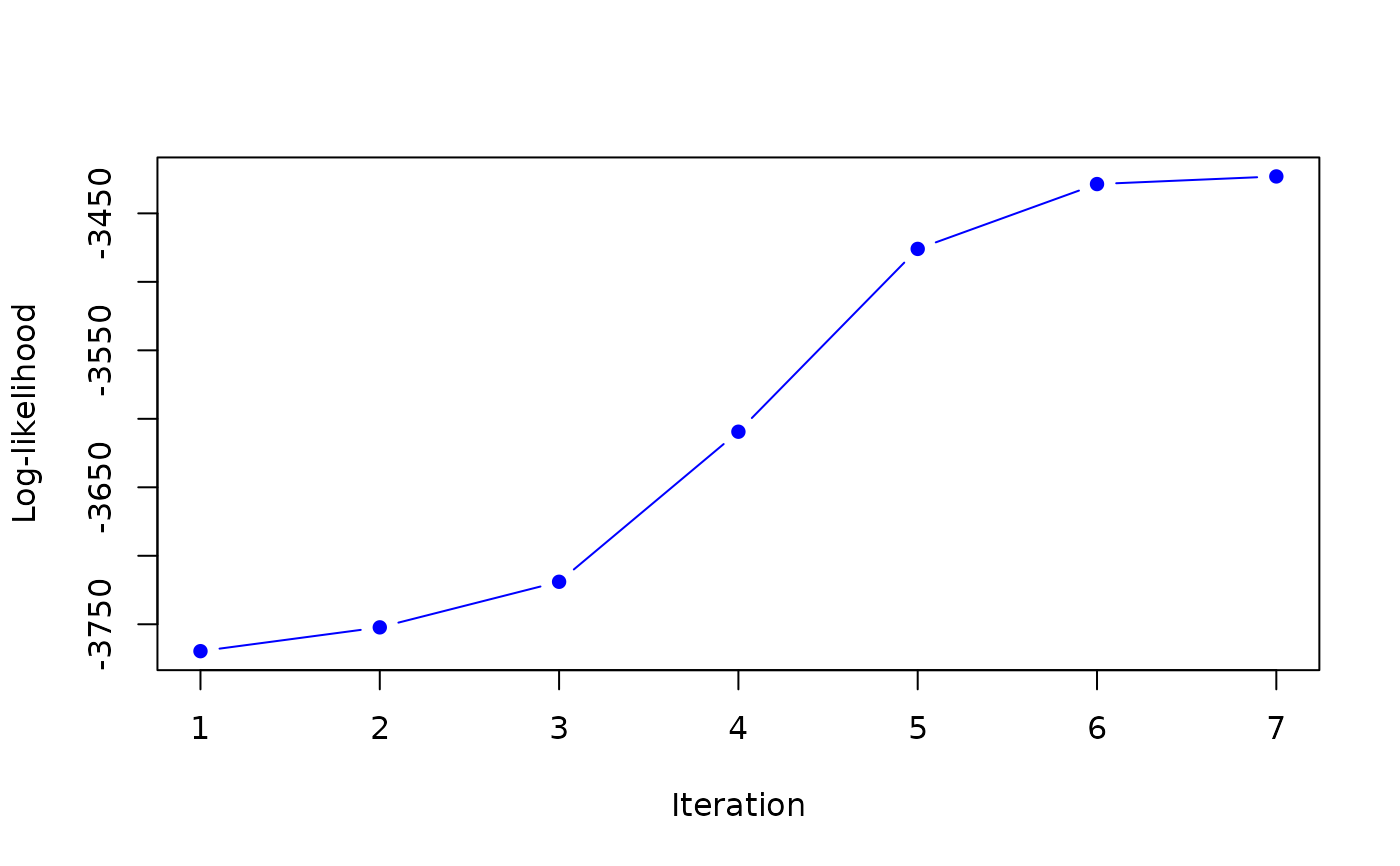#> it 8: loglik = -3422.515
#> weights: 0.497766 0.502234 
#>